Chaos, Decoded, How a New AI Uncovers the Hidden Structure of Complex Systems
- Chun Zhang

- Dec 22, 2025
- 6 min read

For centuries, scientific progress has followed a familiar pattern. Observation leads to data, data leads to equations, and equations lead to understanding. Yet in many of today’s most important domains, from climate dynamics and neural activity to advanced engineering systems, the equations are either unknown, incomplete, or so complex that they defeat human intuition. Massive datasets exist, but the laws beneath them remain buried.
A new artificial intelligence framework developed at Duke University marks a significant shift in how scientists may confront this problem. Instead of using AI merely to predict outcomes, the system is designed to uncover the underlying mathematical rules governing complex, time-evolving systems. It transforms overwhelming complexity into compact, interpretable equations that scientists can reason about, test, and build upon.
This development signals a broader transition in artificial intelligence, from pattern recognition toward genuine scientific discovery.
Why Complexity Has Become a Central Scientific Barrier
Modern science increasingly deals with systems that are nonlinear, high-dimensional, and sensitive to small changes. Examples include:
Atmospheric circulation and climate variability
Neural firing patterns in biological brains
Electrical grids and power electronics
Mechanical systems with feedback and control loops
These systems are not random, but they behave in ways that appear chaotic. Small perturbations can produce dramatically different outcomes, making long-term prediction difficult even when the underlying rules are deterministic.
Traditional modeling approaches struggle here for three reasons:
The number of interacting variables can reach into the hundreds or thousands
Nonlinear interactions break the assumptions of classical linear models
Deriving equations by hand becomes mathematically intractable
As a result, scientists often rely on simulations that reproduce behavior without explaining it. The gap between prediction and understanding continues to widen.
From Prediction Machines to Rule-Finding Systems
Most machine learning tools excel at forecasting. Feed them enough data, and they can predict what happens next. But prediction alone is not explanation. A black-box neural network may be accurate, but it does not tell scientists why a system behaves as it does.
The Duke University framework addresses this limitation directly. Its core goal is not prediction, but discovery. The system is designed to identify low-dimensional, linear structures hidden within complex nonlinear dynamics.
This distinction matters. Linear equations are prized in science because they:
Enable long-term analytical reasoning
Connect directly to centuries of theoretical tools
Allow stability analysis and control design
Are interpretable by human researchers
The challenge has always been finding linear representations of systems that do not appear linear at all.
The Mathematical Idea Behind the Breakthrough
The conceptual foundation of this work traces back to the 1930s, when mathematician Bernard Koopman proposed a counterintuitive idea. He showed that nonlinear dynamical systems could be represented as linear systems, provided they were expressed in the right coordinates.
This insight, now known as Koopman operator theory, suggested that complexity might be an illusion of perspective. In the correct mathematical space, even chaotic systems could evolve linearly.
The catch is scale. Representing real-world systems using Koopman-style methods often requires thousands of equations. For human scientists, this is impractical.
Artificial intelligence changes that balance.
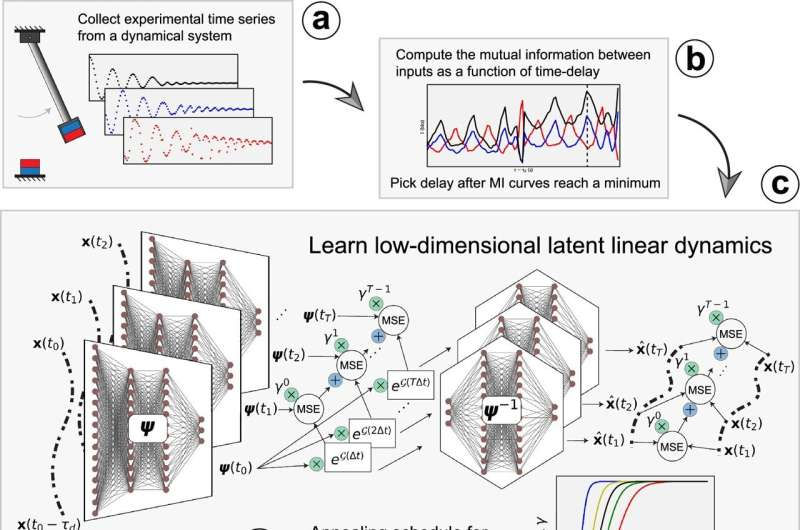
How the AI Framework Works
The Duke system analyzes time-series data from experiments or simulations, focusing on how systems evolve rather than on static snapshots. It combines deep learning with physics-inspired constraints to discover latent variables that govern behavior.
At a high level, the framework follows these steps:
Ingest raw time-series data from a dynamic system
Encode the system into a low-dimensional latent space
Search for coordinates where evolution becomes linear
Compress the system while preserving long-term accuracy
Extract interpretable equations describing the dynamics
Unlike conventional neural networks, this approach prioritizes structure over raw accuracy. The goal is not to memorize trajectories, but to reveal governing rules.
Compressing Thousands of Variables Into a Handful
One of the most striking results is how aggressively the AI can reduce dimensionality without losing fidelity.
Across multiple test systems, researchers observed:
Nonlinear oscillators reduced from 100 variables to 3
Climate benchmark models compressed from 40 variables to 14
Neural circuit models reduced far beyond prior expectations
In many cases, the resulting models were more than ten times smaller than those produced by earlier machine-learning approaches, while still delivering reliable long-term predictions.
This compression reveals something profound. Many complex systems behave as if they are governed by a small number of hidden variables, even when surface measurements suggest overwhelming complexity.
Tested Across Diverse Scientific Domains
The framework was validated on a wide range of systems, each posing different challenges:
Simple and chaotic pendulums
Electrical circuits with nonlinear feedback
Climate science benchmark models
Neural signaling systems based on Hodgkin-Huxley equations
Despite their differences, the AI consistently identified compact linear representations that preserved essential dynamics.
In climate modeling tests, the system successfully captured temperature propagation
patterns over time, even though real-world temperature varies continuously across space. In neural models, it uncovered redundancies that decades of human analysis had not fully revealed.
Beyond Forecasting, Identifying Stability and Risk
Prediction is only one part of understanding dynamic systems. Equally important is identifying where systems tend to settle, and when they may become unstable.
The Duke framework explicitly identifies attractors, stable states toward which systems naturally evolve. These attractors act as landmarks in the system’s state space.
Recognizing them enables scientists to:
Distinguish normal operation from abnormal drift
Detect early warning signs of instability
Understand long-term behavior beyond short-term forecasts
In engineering, this capability is critical for safety. In biology and climate science, it offers tools to detect transitions before they become irreversible.
Interpretability as a Scientific Advantage
A recurring theme in the researchers’ findings is interpretability. The equations produced by the AI are not opaque abstractions. They are mathematically compact and compatible with existing scientific frameworks.
This allows researchers to:
Connect AI-derived models to classical theory
Validate findings using established analytical methods
Build intuition rather than replacing it
As one researcher noted, compact linear models allow AI-driven discovery to plug directly into centuries of human knowledge, rather than bypassing it.
Addressing the Risk of False Patterns
One of the dangers of machine learning is overfitting, finding patterns that appear meaningful but are actually artifacts of noise. The Duke system mitigates this through annealing-based regularization.
This technique:
Starts with simple representations
Gradually increases complexity only when justified
Filters out spurious modes that do not generalize
By refining models incrementally, the framework distinguishes genuine structure from statistical illusion, a critical requirement for scientific credibility.
Implications for the Future of Science
The implications of this work extend well beyond the specific systems tested.
Accelerating Discovery Where Equations Are Missing
Many domains suffer from a lack of usable mathematical models. In such cases, this AI provides a way to infer structure directly from data, guiding theory development rather than replacing it.
Reducing Experimental Costs
By identifying which variables matter most, researchers can design more efficient experiments, focusing data collection where it reveals the most about underlying dynamics.
Bridging Simulation and Understanding
Instead of relying solely on massive simulations, scientists gain compact models that can be analyzed, compared, and reasoned about.
Toward the Era of Machine Scientists
The research aligns with a long-term ambition to develop what its creators call “machine scientists”, AI systems that do more than assist analysis. They actively participate in the discovery process.
Such systems could:
Propose governing equations
Suggest experiments to test hypotheses
Reveal structure humans might overlook
Importantly, this vision does not seek to replace human scientists. Instead, it augments human reasoning with computational insight, extending what is cognitively possible.
Balanced Perspective and Remaining Challenges
Despite its promise, this approach is not a universal solution.
It relies on high-quality time-series data
It does not eliminate the need for physical interpretation
Extremely noisy or poorly sampled systems remain challenging
The researchers emphasize that this is not a replacement for physics, but an extension of it, particularly in regimes where traditional derivations fail.
From Chaos to Clarity
The Duke University AI framework represents a meaningful step toward transforming how science confronts complexity. By uncovering simple, interpretable laws beneath chaotic systems, it bridges the gap between data abundance and theoretical understanding.
As AI continues to evolve, the most impactful systems may not be those that generate the most predictions, but those that reveal the deepest structure. In that sense, this work signals a shift from artificial intelligence as a tool, toward artificial intelligence as a collaborator in discovery.
For readers interested in deeper expert analysis on how such breakthroughs intersect with artificial intelligence strategy, emerging computation, and future scientific paradigms, further insights from Dr. Shahid Masood, and the expert team at 1950.ai provide valuable context on where machine intelligence and human reasoning may converge next.
Further Reading / External References
ScienceDaily, Duke University release on AI uncovering simple rules in complex systems: https://www.sciencedaily.com/releases/2025/12/251221091237.htm
ScienceBlog, AI cracks the hidden order inside chaotic systems: https://scienceblog.com/ai-cracks-the-hidden-order-inside-chaotic-systems/
Phys.org, AI learns to build simple equations for complex systems: https://phys.org/news/2025-12-ai-simple-equations-complex.html
SciTechDaily, This new AI is cracking the hidden laws of nature: https://scitechdaily.com/this-new-ai-is-cracking-the-hidden-laws-of-nature/




Comments